Core Math Worksheets
Fraction Worksheets
Word Problems
Algebra and Trigonometry
Other Worksheets
Place Value
Percentages
Rounding Numbers
Ordering Numbers
Standard, Expanded, Word Form
Mean Median Mode Range
Ratio Worksheets
Probability Worksheets
Roman Numerals
Factorization, GCD, LCM
Prime and Composite Numbers
Pre-Algebra
Geometry Worksheets
Blank Clocks
Telling Analog Time
Analog Elapsed Time
Greater Than and Less Than
Money
Arithmetic Sequences
Geometric Sequences
Venn Diagram
Graph Worksheets
Measurement & Conversions
Patterns and Puzzles
Color by Number
Holiday & Seasonal
Early Learning
Printables
Calculators
Trig Identities, Tables, Charts and Cheat Sheets
A collection of charts, tables and cheat sheats for trignometry identities. These printable PDFs are great references when studying the trignometric properties of triangles, unit circles, and functions.
Trig Identities
Trigonometry Charts & Tables
Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles, particularly right-angled triangles. Below is a compilation of useful charts and tables of trigonometric identities, formulas, and a trigonometric chart or sometimes informally referred to as trig charts that you can use as reference for solving problems involving trigonometry problems.
Introduction to Trigonometry
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles, particularly right-angled triangles. The term "trigonometry" comes from the Greek words "trigonon", meaning triangle, and "metron", meaning measure. Initially developed to solve problems in astronomy and navigation, trigonometry has since become an important tool in many fields, including mathematics, physics, engineering, architecture, computer science, and even economics.
At its core, trigonometry provides the means to study and calculate angles, distances, and other important properties in both two-dimensional and three-dimensional spaces. Although its applications are vast, trigonometry is often most closely associated with right-angled triangles, where one of the angles is always 90°. The relationships between the sides of these triangles are captured by trigonometric functions, which are necessary in understanding various geometrical and physical phenomena.
What Are The Key Concepts in Trigonometry?
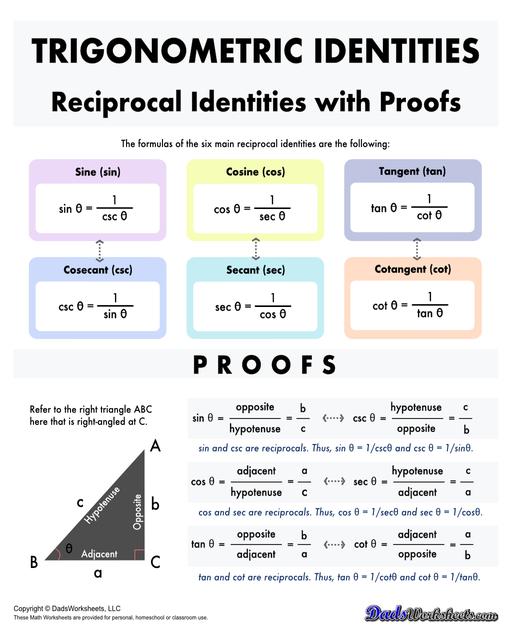
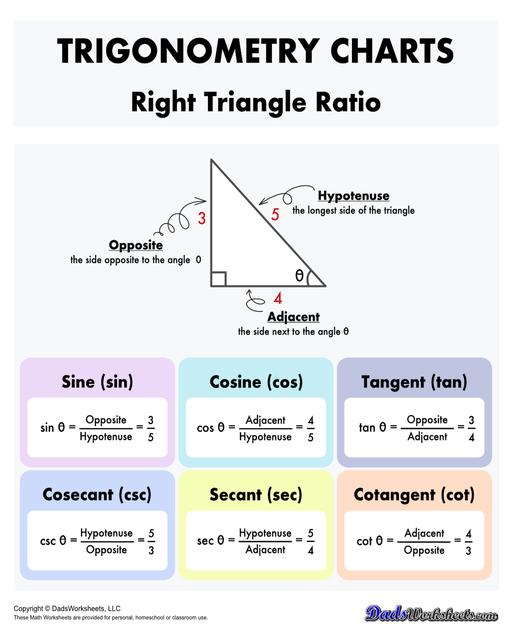
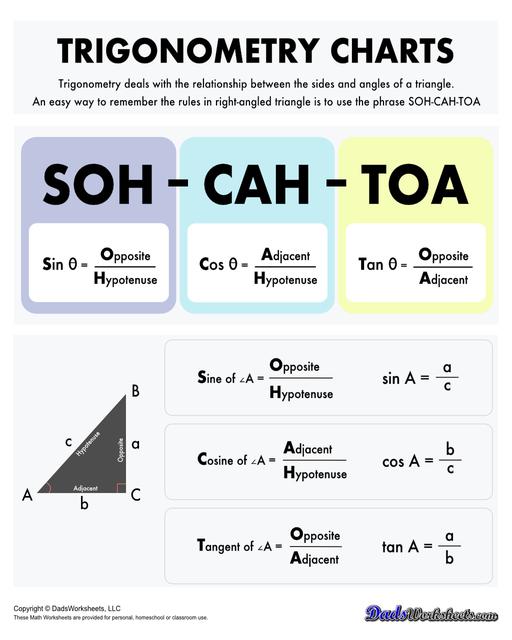
A right-angled triangle is a triangle in which one of the angles is exactly 90°. The longest side of a right-angled triangle is called the hypotenuse, and the other two sides are referred to as the opposite and adjacent sides, depending on the angle of interest. Refer to triangle ABC below.

Understanding Angles
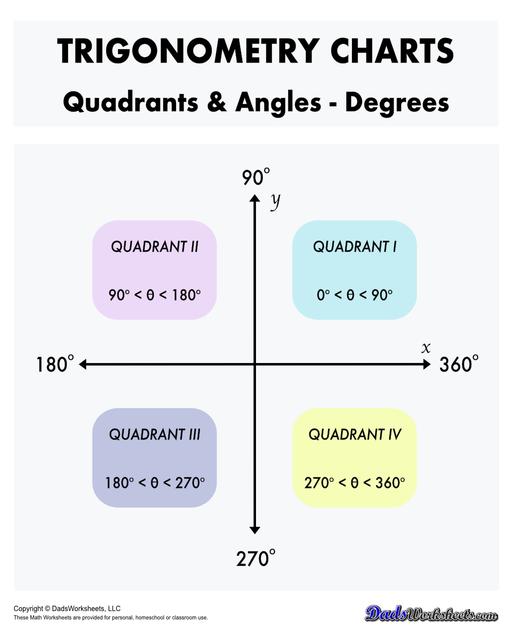
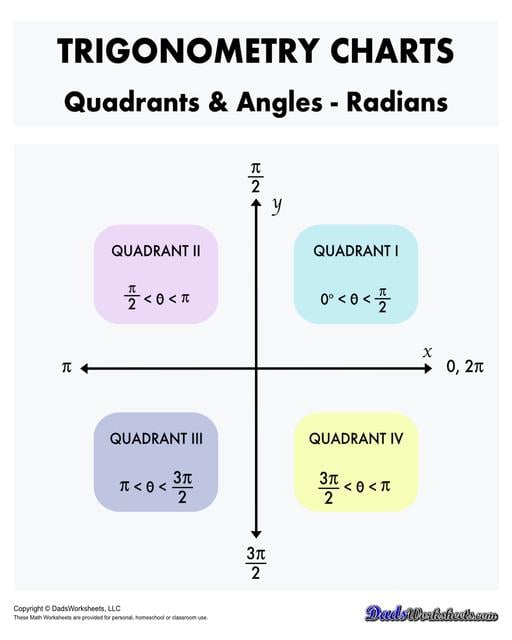
Angles can be measured in two common units: degrees and radians.
Conversion Between Degrees and Radians:
From Radians to Degrees: Multiply by 180/π.
Types of Angles
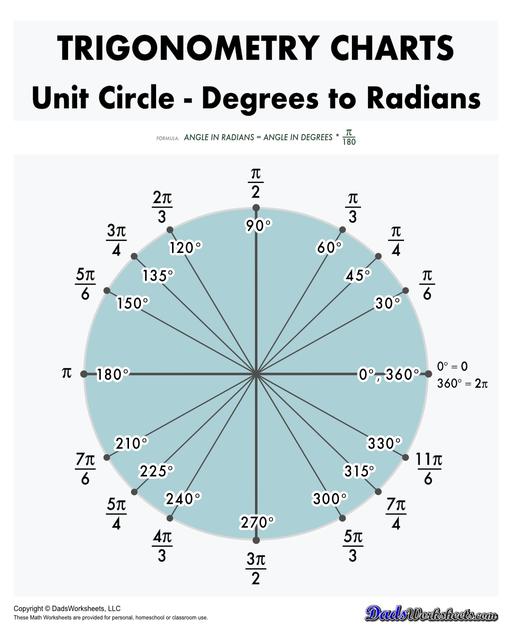
Angles on the Unit Circle
The unit circle is a circle with a radius of 1, centered at the origin of the coordinate plane.
Every angle corresponds to a point on the unit circle, where the x-coordinate is cos(θ) and the y-coordinate is sin(θ) for a given angle θ.
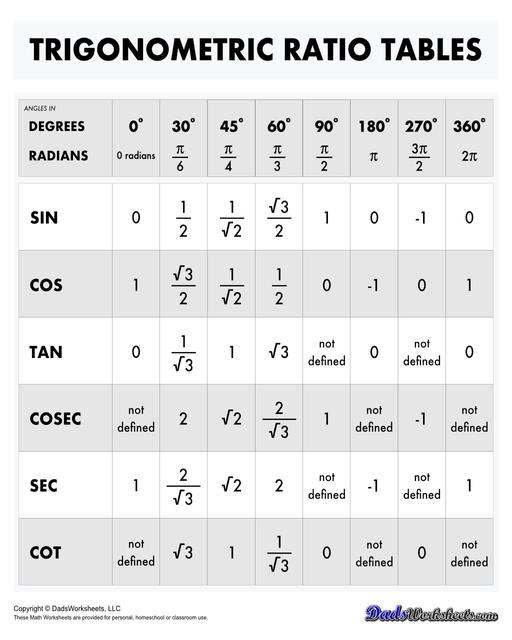
Special Angles and Their Trigonometric Values
There are a few key angles whose sine, cosine, and tangent values are particularly important to memorize, as they frequently appear in calculations. These angles are 0°, 30°, 45°, 60°, and 90°, as well as their corresponding radian values.
Trigonometric Right Triangle Ratios
The key to trigonometry lies in the six trigonometric functions, which define the relationships between the angles and sides of a right-angled triangle. These functions are based on the ratio of the lengths of two sides of the triangle relative to one of its angles (other than the right angle). The primary trigonometric ratios are:
The Unit Circle
One of the most important concepts in trigonometry is the unit circle, a circle with a radius of 1 centered at the origin of the coordinate plane. The unit circle provides a way to define the trigonometric functions for all angles, not just those in right-angled triangles. On the unit circle, any point can be represented by its coordinates (x,y), where:
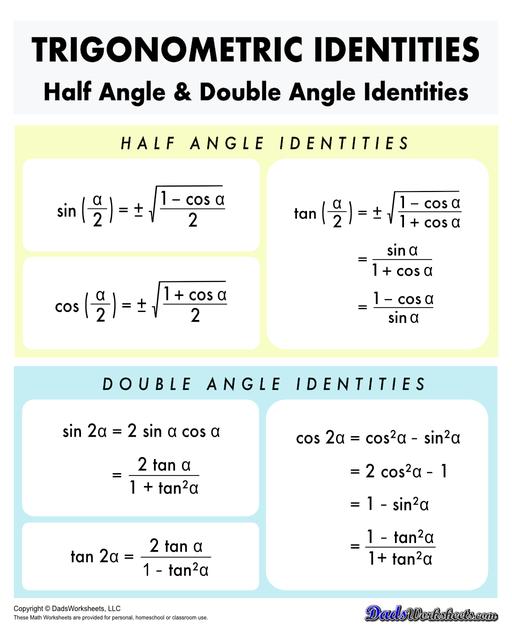
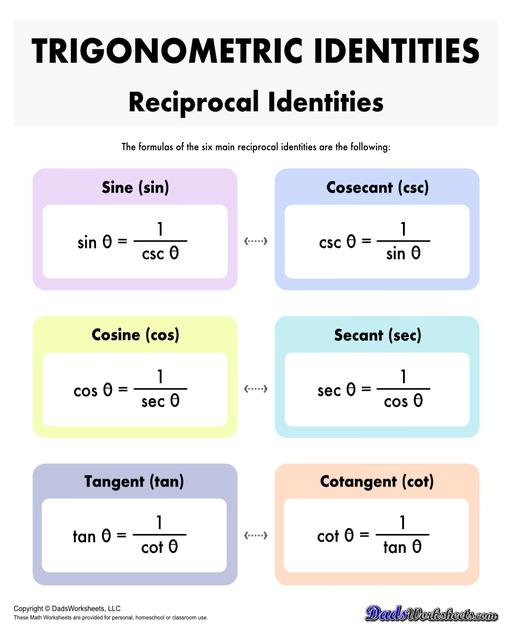
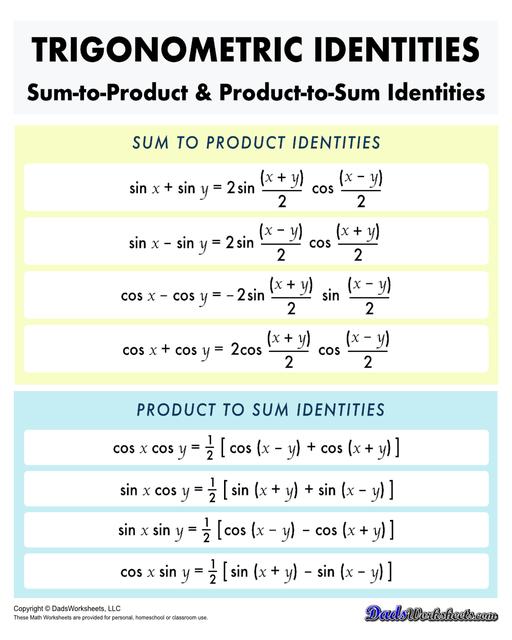
Trigonometric Identities
Trigonometric identities are equations that involve trigonometric functions and are true for all values of the variables involved. These identities are powerful tools for simplifying expressions, solving equations, and transforming trigonometric functions. Some of the most important identities include:
Pythagorean Identities: state that no matter what the value of θ is, sin2θ + cos2θ is equal to 1. These identities are used in solving many trigonometric problems where one trigonometric ratio is given and the other ratios are to be found.
Reciprocal Identities: state that each trigonometric function is a reciprocal of another trigonometric function. The sine function is the reciprocal of the cosecant function and vice-versa; the cosine function is the reciprocal of the secant function and vice-versa; cotangent function is the reciprocal of the tangent function and vice-versa.
Angle Sum and Difference Identities: are used to find the value of the trigonometric functions at specific angles where it is easier to express the angle as the sum or difference of unique angles (0°, 30°, 45°, 60°, 90°, and 180°).
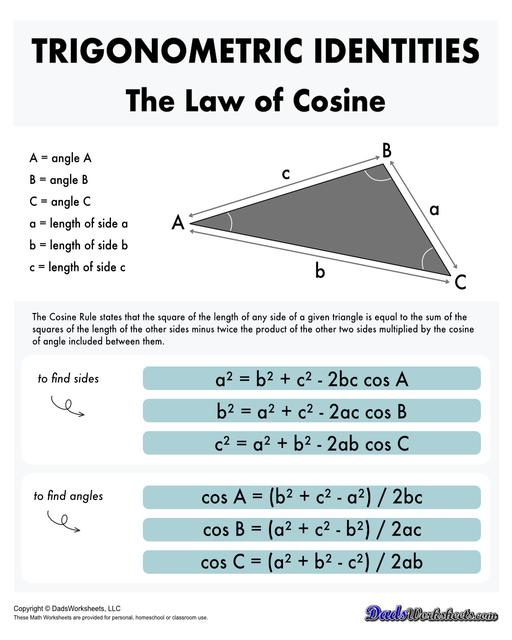
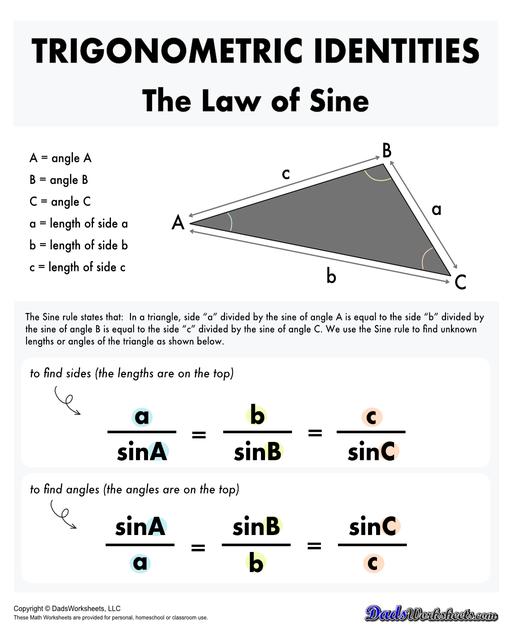
Law of Sines and Law of Cosines
The Sine rule states that: In a triangle, side “a” divided by the sine of angle A is equal to the side “b” divided by the sine of angle B is equal to the side “c” divided by the sine of angle C. we use the Sine rule to find unknown lengths or angles of a non right-angled triangle.
The Cosine rule, on the other hand, states that the square of the length of any side of a given triangle is equal to the sum of the squares of the length of the other sides minus twice the product of the other two sides multiplied by the cosine of angle included between them.
The Importance of Trigonometry Charts and Tables
One of the most valuable tools for quickly solving trigonometric problems is the use of trigonometry charts and tables. These resources provide a quick reference to the values of trigonometric functions for various angles, making it easier to perform calculations and solve complex problems. Let’s explore the importance of trigonometry charts and tables and how they contribute to academic applications.
One of the primary advantages of using trigonometry charts and tables is the speed and efficiency they bring to calculations. Rather than having to manually compute trigonometric values for each angle from first principles, students can quickly look up values in a table for common angles (e.g., 30°, 45°, 60°, etc.). This significantly reduces the amount of time spent on routine calculations, allowing us to focus on solving more complex aspects of problems. When problems that involve angles such as 30°, 45°, 60°, or 90°, it's helpful to have a ready-made reference for standard values. Trigonometry charts and tables enable users to simplify calculations by providing values on hand to make the process of solving problems more straightforward. For example, by using a trigonometric chart, we can quickly find the sine, cosine, or tangent of common angles without recalculating them every time.
Moreover, when performing trigonometric calculations, especially in professional or academic settings, accuracy is paramount. Charts and tables provide exact values of trigonometric functions for standard angles, ensuring that results are consistent across calculations. This reduces the risk of human error that can occur when manually calculating trigonometric values, especially when dealing with irrational numbers.
Key Takeaways for a Strong Foundation:
- Master the basic trig functions (sine, cosine, tangent, and their reciprocals).
- Understand the unit circle and how it relates to the values of the trigonometric functions.
- Learn the trigonometric identities and how to manipulate them.
- Be able to solve simple trigonometric equations.
- Learn how to apply the Law of Sines and Law of Cosines for non-right triangles.
More Math Charts
If you are looking for more math charts, be sure to check out our main charts page! You will find lots of printable charts like the Multiplication Charts or our unique Fraction Chart that you can use for learning and teaching. All of these are high quality PDF files that you can print anytime.