Trigonometry

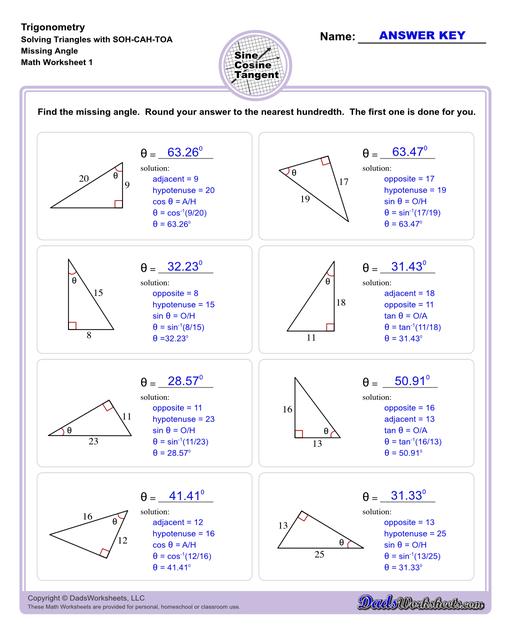
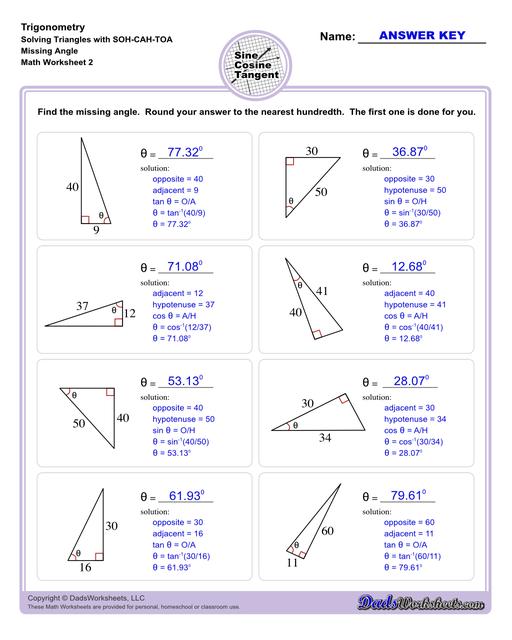
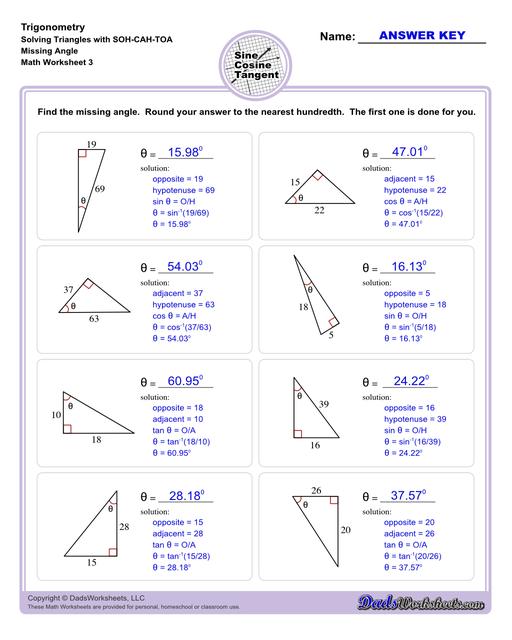
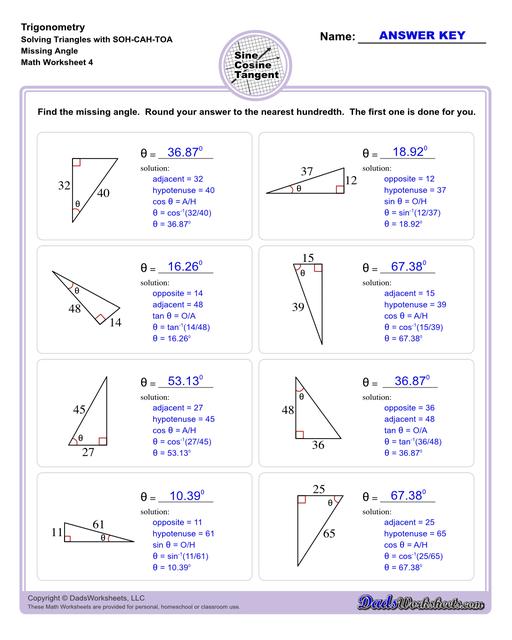
10th and 11th grade trignometry problems with triangles using the sine, cosine, tangent functions. These worksheets include problems involving right-angled triangles and functions are used to solve for the other interior angles.

Trigonometry Worksheets

The trigonometry worksheets on this page cover topics that are introduced mostly in 10th or 11th grade as part of typical math curricula such as solving problems with triangles using the sine, cosine, tangent functions. More specifically, right-angled triangles, where one of the internal angles is 90°.

While understanding the theory behind trigonometry is essential, practice is where the magic happens. One of the best ways to reinforce what students learn in class is by using trigonometry worksheets. These worksheets provide structured practice and help students internalize key concepts through repetition, which leads to better retention and a deeper understanding of the material.

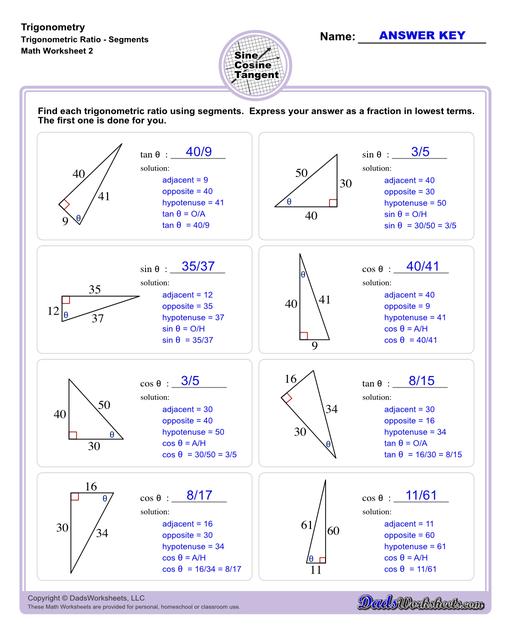
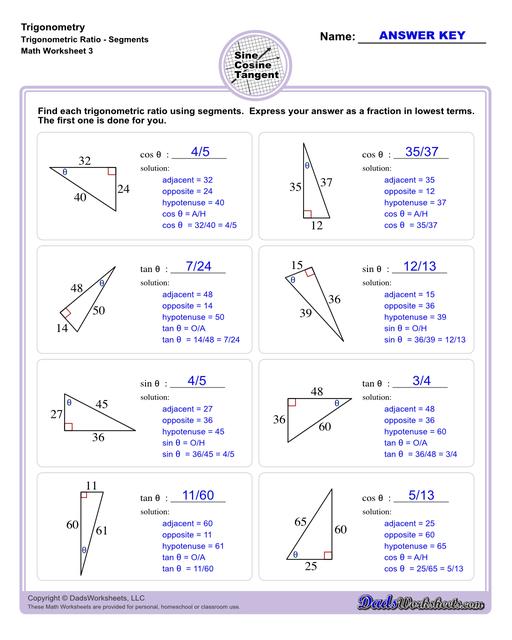
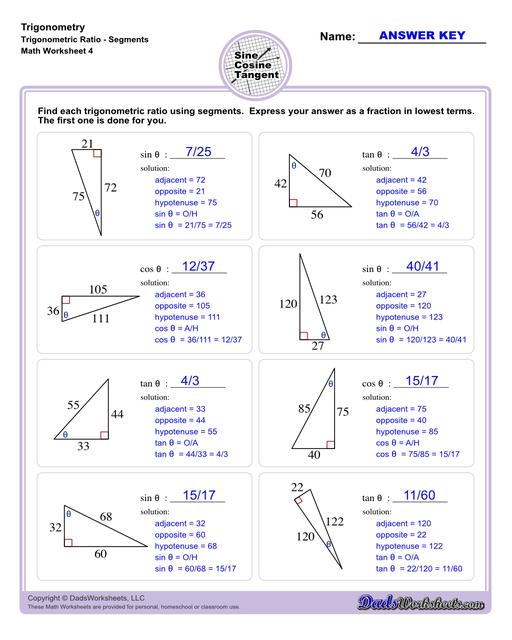
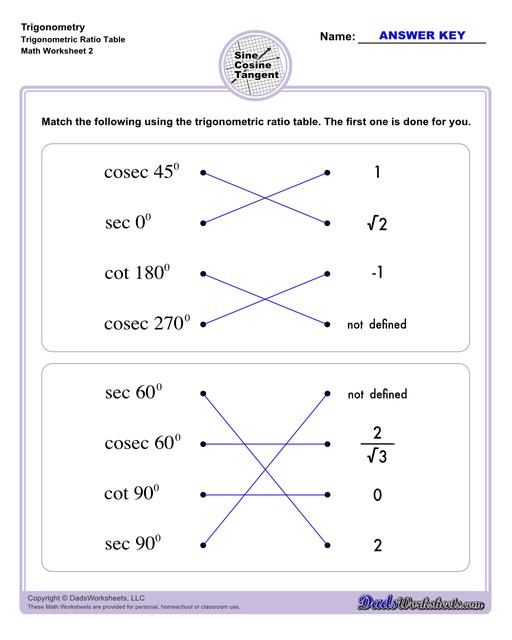
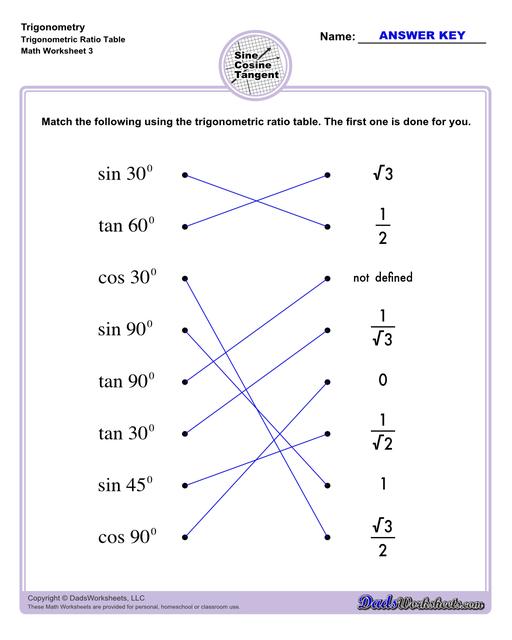
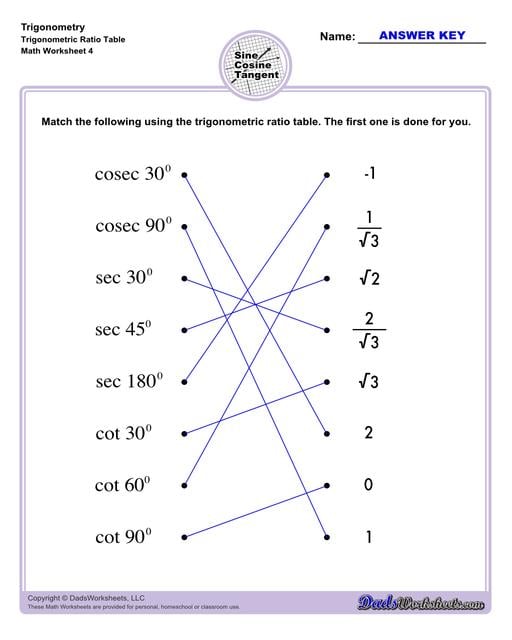
The worksheets on this page start with exercises involving primary trigonometric ratios. Then the succeeding sets will let students solve for unknown side lengths or angles in a triangle. Multi-step problems and word problems are also available. All worksheets include answers keys and solutions, all of which can be found on the second page of the PDF file. You may also print any of our trig charts for concept help to easily master trigonometry while doing the worksheets.

More worksheets will be added in the future so be sure to come back and visit this page from time to time.

Pythagorean Theorem vs. Trigonometry

When studying right-angled triangles, students often come across two key concepts: the Pythagorean Theorem and trigonometry. Both are powerful tools for solving problems, but they serve different purposes. Understanding when and how to use each can make math feel a lot less intimidating and even fun! Continue reading to know how these two mathematical approaches compare, when each is best used, and how they can complement each other in the classroom.

First, let’s revisit the Pythagorean Theorem, one of the most fundamental principles in geometry.

Consider three squares corresponding to the three sides of the right triangle abc... The area of the square corresponding to the hypotenuse is equal to the sum of area of the squares corresponding to the other two sides.

Here’s a diagram to visualize the theorem…

The theorem states that: a² + b² = c²

The Pythagorean theorem establishes the relationship between the sides of a right triangle. It is an important rule that applies only to right-angled triangles. It says that the square on the hypotenuse is equal to the sum of the squares on the other two sides.

Using the Pythagorean theorem, you can find the hypotenuse (the longest side) of a right triangle if you know the length of the other two sides. Or, if you know the length of the hypotenuse and the length of one of the sides, you can find the other side.

Now, let’s talk about trigonometry.

Trigonometry goes beyond the Pythagorean Theorem by involving the angles of a triangle, not just the sides. The most common trigonometric ratios are:

• Sine (sin) = opposite/hypotenuse
• Cosine (cos) = adjacent/hypotenuse
• Tangent (tan) = opposite/adjacent

These ratios are useful when you’re dealing with angles and sides of a right triangle, especially if you have at least one angle (except for the right angle) and one side length. Trigonometry allows you to calculate unknown sides or angles.

When to Use Trigonometry:

• Finding unknown angles: When you know one side and one non-right angle, trigonometry is your best tool.
• Solving for sides: You can use trigonometric ratios when you have an angle and one side to solve for other unknown sides.

For students, understanding both methods can be incredibly empowering. Teachers can introduce them in stages, starting with the Pythagorean Theorem for basic side-length problems and then moving to trigonometry for more dynamic problems involving angles. A good approach is to show how both concepts can work together:

• Use the Pythagorean Theorem to find the length of one side, then use trigonometry to find an angle.
• Use trigonometry to find a missing side, and then use the Pythagorean Theorem to verify your result.

So, if we know the length of two sides of a triangle and we need to calculate the third, we can use Pythagoras’ Theorem. However, if we know only one side length and one of the internal angles, then Pythagoras is no use to us on its own and we need to use trigonometry.

How to Get Started with Trigonometry

Starting with trigonometry can feel like stepping into unfamiliar territory, so I gathered a simple guide to help you take your first steps into this essential branch of mathematics.

Understand the Basics of Geometry

Before diving into trigonometry, make sure you're comfortable with some key concepts from geometry:

• Right triangles: Trigonometry primarily deals with right-angled triangles, so understanding what makes a triangle "right" (one 90° angle) is crucial.
• Angles: Trigonometry is all about angles and their relationships to sides of triangles. Familiarize yourself with the types of angles:

Review on Right-Angled Triangles:

A right-angled triangle has a single right angle as shown below. By definition, that means that all three sides cannot have the same length.

• The right angle is indicated by the little box in the corner.
• The other angle is indicated by θ.
• The side opposite the right angle, which is the longest side, is called the hypotenuse.
• The side opposite θ or the angle you're working with is called the opposite.
• The side next to θ, but is not the hypotenuse is called the adjacent.

Key Trigonometric Functions: Sine, Cosine, and Tangent

• Sine (sin): The ratio of the side opposite the angle to the hypotenuse
• Cosine (cos): The ratio of the adjacent side to the hypotenuse
• Tangent (tan): The ratio of the opposite side to the adjacent side

It’s helpful to start by memorizing these relationships and practicing with simple right triangles. Again, if you know the lengths of two sides of a right triangle, you can use these functions to find the third side or the angles.

To remember these ratios, many students use the classic mnemonic: SOH-CAH-TOA

• SOH: Sine = Opposite / Hypotenuse
• CAH: Cosine = Adjacent / Hypotenuse
• TOA: Tangent = Opposite / Adjacent

This will help you recall which sides correspond to each trigonometric function when solving right triangles.

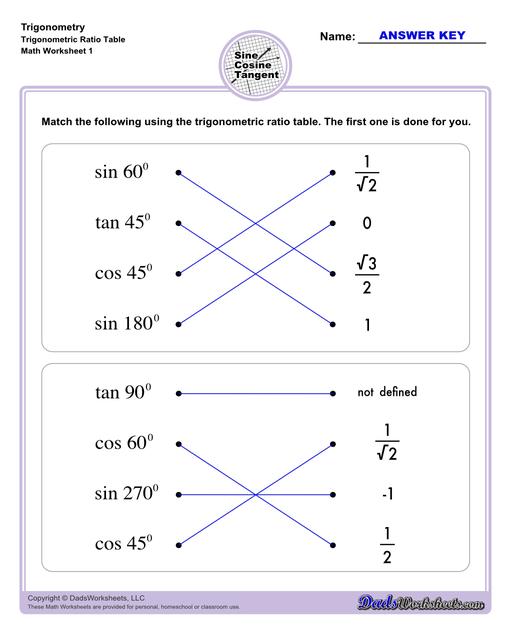
Explore the Unit Circle

The unit circle is one of the most important concepts in trigonometry. It's a circle with a radius of 1, centered at the origin (0,0) of a coordinate plane. The unit circle helps visualize the trigonometric functions for all angles, not just those in right triangles.

In the unit circle:

• The x-coordinate of a point on the circle gives you the cosine of the angle.
• The y-coordinate gives you the sine of the angle.

Here’s how it works:

• Every point on the unit circle corresponds to an angle, and the x and y coordinates of that point represent the cosine and sine of the angle, respectively.
• This means that for any angle θ, you can find:

Understanding the unit circle will allow you to extend the concepts of sine, cosine, and tangent beyond right triangles and into all angles, even those larger than 90°. This leads to the idea of periodicity in trigonometric functions, where sine, cosine, and tangent repeat at regular intervals.

Start by memorizing key angles on the unit circle, like 30°, 45°, and 60°. These will come up often and will help you build a stronger understanding of the relationships between angles and their sine and cosine values.

Practice Problem

To get hands-on experience, start solving problems involving right triangles.

Example: Given a right triangle where the adjacent side is 4 units. and the hypotenuse is 5 units, find the cosine of the angle.

As you solve more problems, you’ll become familiar with how to use these functions and apply them to find unknown angles or side lengths.

Trigonometric Identities

As you progress, you’ll encounter trigonometric identities, which are equations that relate trigonometric functions to each other. The most common identities you’ll use early on are:

• Pythagorean Identity: This is the foundation of many trigonometric problems, especially when you need to find missing values or simplify expressions.
• Reciprocal Identities: state that each trigonometric function is a reciprocal of another trigonometric function.

There are a lot more identities in trigonometry and getting comfortable with these identities will be important for simplifying trigonometric expressions and solving more complex problems later. Read more about trigonometric identities on our Trig Identities, Tables, Charts and Cheat Sheets page.