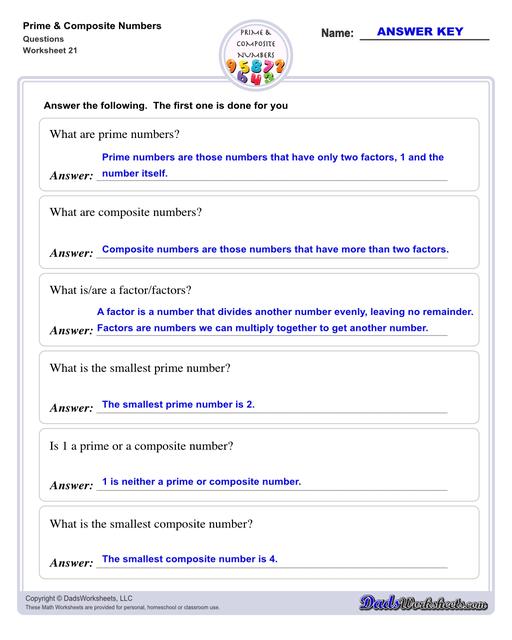
Prime and Composite Numbers

Prime and composite numbers are differentiated based on the number of factors they have. These worksheets require students to identify prime or composite numbers, and they can use one of a collection prime or composite number charts to help!

Factors and How To Find Them

Before we start with prime and composite numbers, let us first understand what factors are and how to find them.

There are two methods for finding factors:

• Through multiplication - factors are defined as numbers we can multiply together to get another number. Let us consider the number 6. 6 can be a product of 1 and 6, and 3 and 2. As a result, the factors of 6 are 1, 2, 3, and 6.
• Through division - a factor is a number that divides another number evenly, leaving no remainder. Let us consider number 6 again. 6 can be divided by 1, 2, and 3 evenly. So the factors of 6 if we use division is 1, 2, 3, and 6.

Let’s try some examples.

Example 1: Find the factors of number 8.

Work from the outside in. Start dividing the number with the number itself then proceed with the next number that will divide it leaving no remainder.

8/8 = 1

8/4 = 2

8/2 = 4

8/1 = 8

Therefore, the factors of number 8 are 1, 2, 4, and 8.

These numbers are also called the divisors of 8. Factors of a number are also called divisors of that same number. The divisor of a number is the value that divides the number into exact parts, in other words, has a remainder of 0.

Another way of finding the factors of a number is through multiplication.

1x8 = 8

2x4 = 8

Here, the numbers that will give a product of 8 are the factors, which are also 1, 2, 4, and 8.

Example 2: Find the factors of 11.

11/1 = 11

11 is a prime number. It has only two factors, 1 and the number itself, which is 11.

Example 3: Find the factors of 36.

36/36 = 1

36/18 = 2

36/12 = 3

36/9 = 4

36/6 = 6

36/4 = 9

36/3 = 12

36/2 = 18

36/1 = 36

The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.

If we use multiplication, what numbers will give a product of 36?

1x36 = 36

2x18 = 36

3x12 = 36

4x9 = 36

6x6 = 36

We got the same factors ~ 1, 2, 3, 4, 6, 9, 12, 18, and 36.

Take note that only positive numbers, whole numbers, and non-fractional numbers are considered when we are looking for factors.

Now that we already know what factors are and how to find them, we can easily distinguish the difference between prime and composite numbers. Read on…

What Are Prime and Composite Numbers?

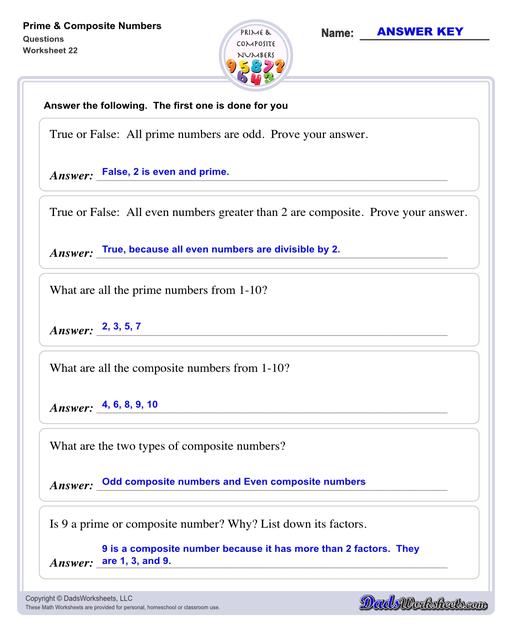
Prime numbers are numbers that have only two factors, 1 and the number itself. For example, the smallest prime number is 2. It has only two factors, 1 and the number itself, which is 2. Any number that does not follow this is termed a composite number, which can be factored into other positive integers. Some other examples of prime numbers include 3, 5, 7, 11, 13, and so on.

Meanwhile, composite numbers are those numbers that have more than two factors. For example, the smallest composite number is 4. It has more than two factors. They are 1, 2, and 4. Numbers that are not prime are composite because they are divisible by more than two numbers. Other examples of composite numbers are 6, 8, 9, 10, and so on.

Also, we can say that except for 1, the remaining numbers are classified as prime and composite numbers. All prime numbers are odd numbers except 2, 2 is the smallest prime number and is the only even prime number.

So all whole numbers (except 0 and 1) are either prime or composite.

You may print this Prime and Composite Numbers Chart 1-100 to easily visualize what we discussed above. Other versions of charts are available too. You can choose to print from our 12 variations of charts in pdf format, including the Prime Numbers Chart and the Composite Numbers Chart, and a lot more.

Is 0 and 1 Prime or Composite?

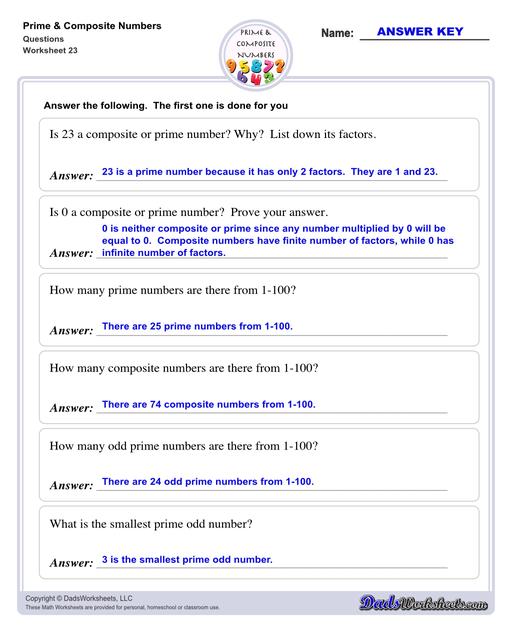
0 and 1 are neither prime nor composite.

Any number multiplied by 0 will be equal to 0, which gives it more than 2 factors. So 0 is not a prime number. It is not a composite number either because all composite numbers have a finite number of factors, while 0 has an infinite number of factors.

1 is neither a prime number nor a composite number also because it has only 1 factor which is 1. Recall the definition of prime number, which states that a number should have exactly two factors, and composite number which states that a number should have more than 2 factors, number 1 has one and only one factor. Thus 1 is not considered a prime or a composite number. It is a unique number.

Things To Remember About Prime and Composite Numbers

• 2 is the smallest prime number.
• 3 is the smallest prime odd number.
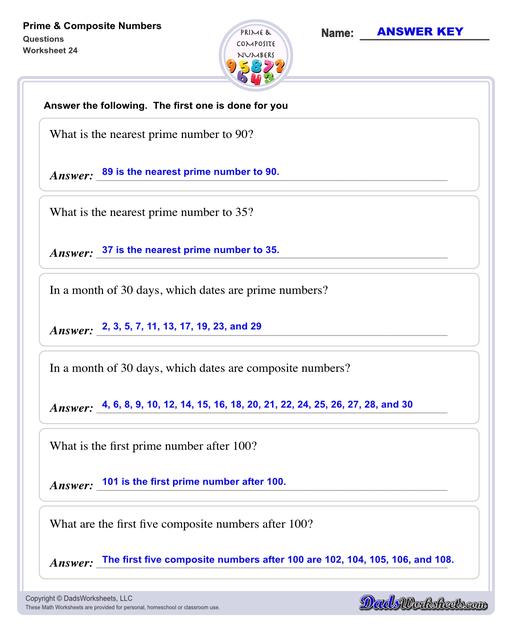
• 11 is the smallest 2-digit prime number.
• 101 is the smallest 3-digit prime number.
• 4 is the smallest composite number.
• 10 is the smallest 2-digit composite number.
• 100 is the smallest 3-digit composite number.
• All even numbers greater than 2 are composite.
• Not all prime numbers are odd. 2 is prime and an even number.
• 0 and 1 are neither prime nor composite numbers.
• There are 25 prime numbers from 1-100.
• There are 74 composite numbers from 1-100.
• There are 24 odd prime numbers from 1-100.
• All integers have a finite number of factors.
• A number’s factor is always less than or equal to the number. It can never be bigger than the number.
• Factors are found by employing division and multiplication.
• Factors are never decimals or fractions. They are only whole numbers or integers.
• All even numbers have 2 as a factor.
• If the sum of a number's digits is a multiple of 3, that number can be divided by 3.
• 5 is a factor for all numbers that end in 0 and 5.
• All numbers higher than 0 and ending in a 0 have 2, 5, and 10 as factors.
• Every number greater than 1 can be divided by at least one prime number.
• Each composite number can be written as a product of two or more primes.
• Composite numbers are divisible by other composite numbers.
• All composite numbers are always divisible by 1 and the number itself.

Tips and Tricks on Prime and Composite Numbers

• When checking to see whether a number is prime or composite, perform divisibility tests in the following order: from easiest to hardest. The order should be from 2, 5, 3, 11, 7, and 13. If you find that a number is divisible by one of these, you know that it’s composite and you don’t have to perform the remaining tests.
• If a number less than 121 is not divisible by 2, 3, 5, or 7, it’s prime. Otherwise, it’s composite.
• If a number less than 289 is not divisible by 2, 3, 5, 7, 11, or 13, it’s prime. Otherwise, it’s composite.

​ ​