Core Math Worksheets
Fraction Worksheets
Word Problems
Algebra and Trigonometry
Other Worksheets
Place Value
Percentages
Rounding Numbers
Ordering Numbers
Standard, Expanded, Word Form
Mean Median Mode Range
Ratio Worksheets
Probability Worksheets
Roman Numerals
Factorization, GCD, LCM
Prime and Composite Numbers
Pre-Algebra
Geometry Worksheets
Blank Clocks
Telling Analog Time
Analog Elapsed Time
Greater Than and Less Than
Money
Arithmetic Sequences
Geometric Sequences
Venn Diagram
Graph Worksheets
Measurement & Conversions
Patterns and Puzzles
Color by Number
Holiday & Seasonal
Early Learning
Printables
Calculators
Transformation Worksheets
These transformation math worksheets practice rotation, reflection and translation transformations of geometric shapes on a coordinate plane. These worksheets are perfect practice exercises for 5th, 6th and 7th grade geometry students.
Transformation Multiple Choice Worksheets
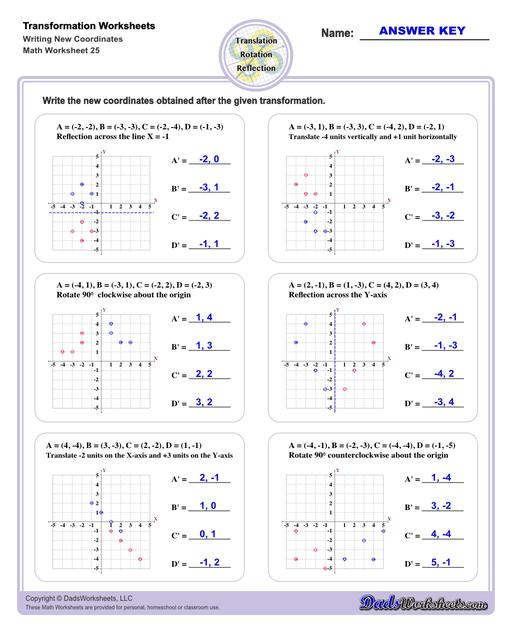
Transformation of Points
Reflection Worksheets
Rotation Worksheets
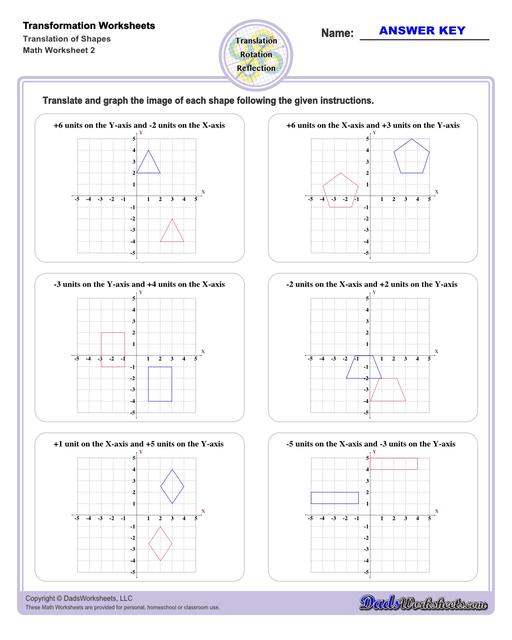
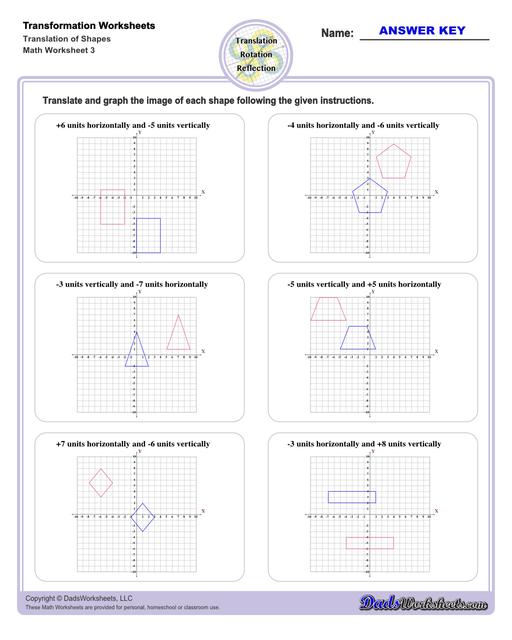
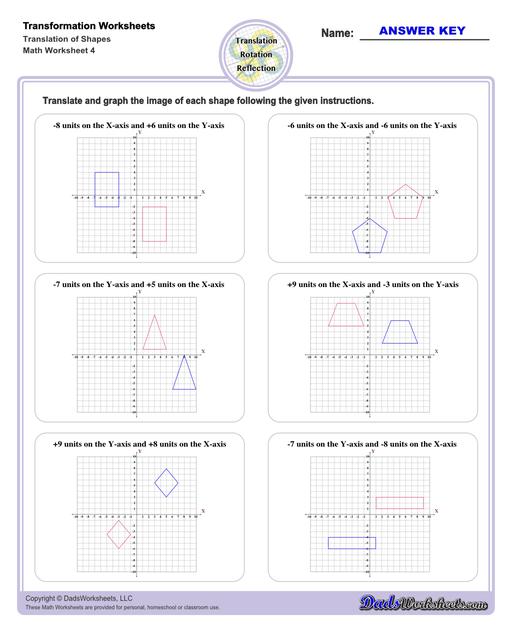
Translation Worksheets
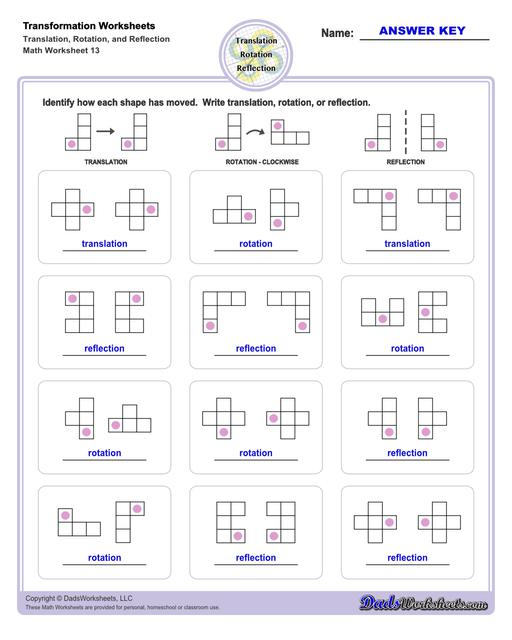
Mixed Transformation Worksheets
Coordinate Transformation Worksheets
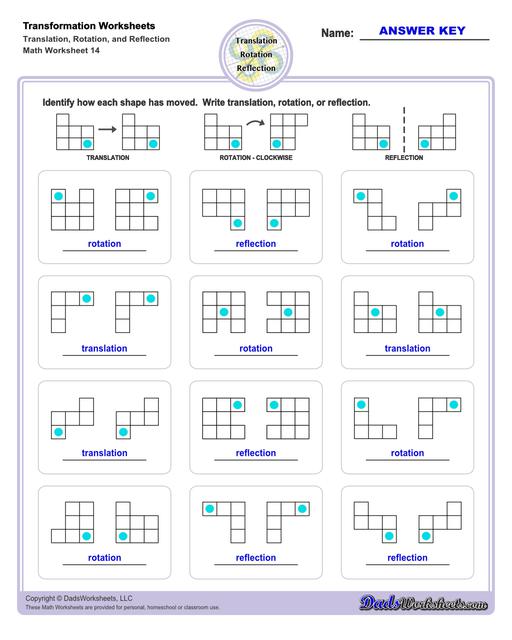
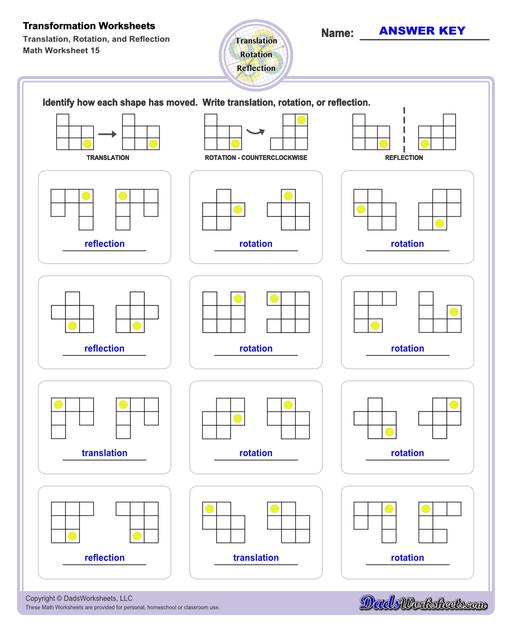
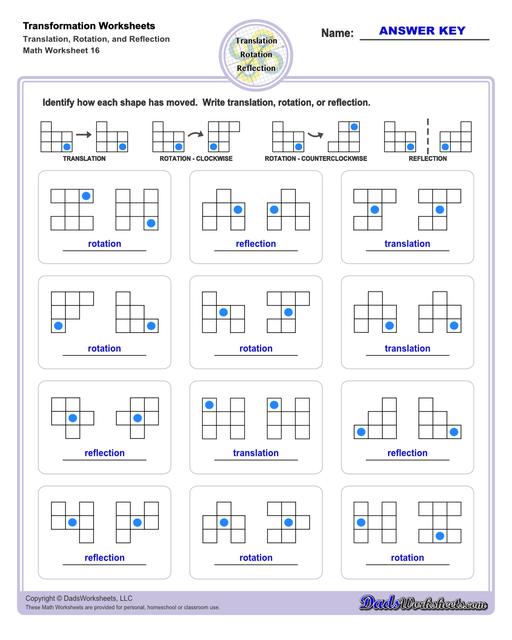
What are Geometric Transformations?
A geoemtric transformation occurs when a system of points (perhaps one point, perhaps a line made up of two points, or perhaps a polygon consisting of multiple points) plotted in a coordinate system is modified in a consistent way. Different types of translations have different names that transforms the points consistently in different ways discussed below.
Translation Transformations
The simplest type of transformation is translation. This is essentially moving (or "sliding") the shape as-is from one position to another. Translation along the x-axis involves adding or subtracting a constant value to the every x coordinate in the shape be transformed, which effectively moves the shape horizontally. Similarly, translation along the y-axis involves adding or subtracting a constant value to the every y coordinate to effect a change in vertical position. Simultaneous translation can happen in both the x-axis and y-axis to move the shape diagonally or "along a line."
After a translation, the new shape will be congruent to the original and retain the same orientation.
Reflection Transformations
Reflection is a type of translation that changes coordinates of a shape by "flipping" a shape over a line. The line of reflection can be any arbitrary line, but it is often a vertical or horizontal line, and often is the x-axis or y-axis. Reflection across one an origin axis has the effect of position the new shape in a different quadrant on the coordinate plane.
To reflect a shape across the x-axis, each y coordinate is inverted in the new shape, in effect (x,y) --> (x,-y).
Similarly, to reflect a shape across the y-axis, each x coordinate is inverted in the new shape, in effect (x,y) --> (-x,y).
After a reflection transformation, the new shape will be congruent to the original, but it will be in a different orientation.
Rotation Transformations
A rotation transformation involves turning a shape as though it were moving around the face of an analog clock. Rotational translations are often visuallized in terms of degrees, and rotational transformations are often about the origin of the coordinate plane. Simple translations about the origin for multiples of 90 degrees look like this...
To rotate 90 degrees around the origin: (x,y) --> (-y,x).
To rotate 180 degrees around the origin: (x,y) --> (-x,-y).
To rotate 270 degrees around the origin: (x,y) --> (y,-x).
Becasue translations for specific multiples of ninety degrees around the origin are actually straightforward manipulations of each coordinate pair that defines a shape, often it is easiest to translate a shape such that the point of rotation will be the origin, then apply the rotational translation, then translate it to its final position.
After a rotation transformation, the new shape will be congruent to the original, but it will be in a different orientation.
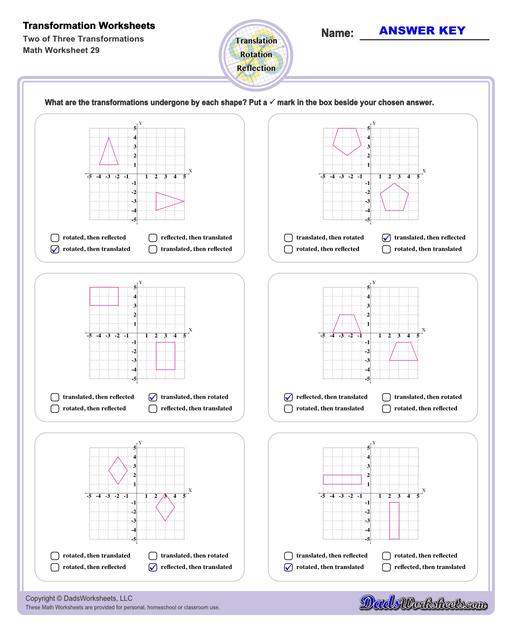
Multiple Transformations
A shape may undergo multiple transformations, and some of the transformation worksheets on this page require solving problems where a shape is reflected, rotated and translated. Solving these problems by hand is usually easiest if each step is performed separately rather than trying to jump to the final transformed form, although once the series of transformation operations is understood, a set of forumulae for modifying each x and y coordinate in the original shape can be determined that performs the composite translation in a single step.